7.4 Ancient Technologies
Crop health is directly related to the health of soils. This lesson teaches students to witness and understand that soil can store water for the needs of humans and plants, and invites them to practice applying modern soil testing techniques. Download the PDF version of the lesson.
Preparation
Grades: 6, 7, 8
This lesson can be taught to each middle school grade with increasing complexity and detail.
In a unit on Pueblo Agriculture, this lesson should be taught after the “Lesson One: People of Corn” and “Lesson Two: Farming Through Drought” lesson plans.
Objectives
- Understand how Hopi culture divides and organizes the labor and responsibility of growing a successful corn crop.
- Explore the mathematics of nutrition and diet: how much corn and how many corn plants are required to feed a family for one year.
- Explore the mathematics of corn productivity: how much garden space is required to feed a family for one year.
Session
Short Session: How a Digging Stick Feeds a Family
Format: One approximately 45 minute session
Opening Circle: Questions and Discussion
Survey students’ understanding and/or opinions by verbally sharing the questions or text in italics. Briefly gather input from the students, while steering the discussion to toward the answers listed below the question.
Families feed themselves in many different ways. In your family, who is responsible for calculating the available money and the groceries needed?
Now imagine, instead, your family calculated how many corn plants and how much land was needed.
Read the following aloud:
Traditionally, in the Hopi culture, the women are responsible for calculating and keeping track of each year’s planting needs, in order to have enough food for the community in coming year. They are responsible for drying and storing seeds from the previous year, ensuring that there is enough corn for both food and ceremony. These are skills and knowledge that the women pass on to their daughters, nieces and grandchildren. Based on the women’s calculations, the men identify and prepare corn field locations, request and receive the correct amount of seed from the women and are responsible for planting the seeds.
— Wall and Masayesva 2004
During this lesson, we will answer these questions (write on whiteboard):
- How much corn would you need to feed yourself and your family for one year?
- How much field space would be needed to plant this amount of corn?
Procedure
- In order to answer these questions, the class will be working through a math narrative as a group. The calculations will be used to estimate:
- the amount of calories (gained from corn) one traditional Hopi family would eat in one year.
- the number of corn plants a Hopi family would need for food and for ceremonies in one year.
- the amount of field space needed to plant this number of corn plants.
- To provide context for the math narrative, read the this description, and the following question, to the group:
A traditional Hopi farmer married to a Hopi woman does not plant for himself but for his wife’s family. Each year before planting begins his wife advises him on the quantities and types of corn needed to provide for the food and ceremonial needs of her family and perhaps others as well. The man in turn tells his wife how many gunnysacks of each type of corn seed that he will need to plant his fields, and she prepares them….(she) must have a clear sense of these varied needs and how best to satisfy them in the coming harvest. Her understanding of the different needs for corn requires intimate knowledge of Hopi culture and religious and ceremonial practice. A woman who can determine the quantities and types of corn needed for the coming year holds a bounty of general knowledge of the Hopi way.
— Wall and Masayesva 2004:443
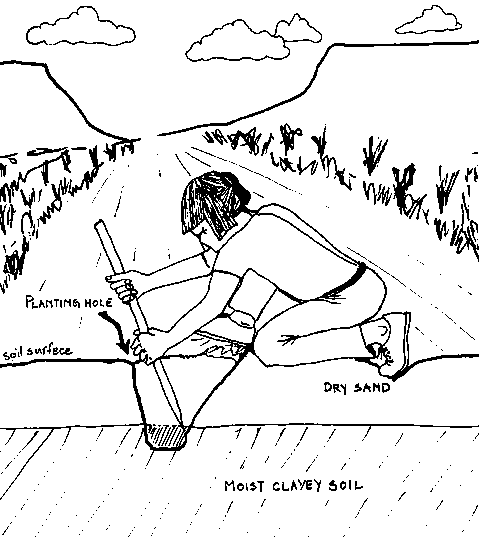
The Hopi people of today grow corn, squash, beans and melons, providing themselves with one third of their diet. Their ancestors grew the same crops, but gained as much as 75% of their diet from corn. All of the corn seed was traditionally planted using the so’ya digging stick (review “Diagram 1: A Planting Hole in a Hopi Maize Field”.)
If your diet was 75% corn, how much corn would you need to plant, and grow successfully, in order to feed yourself and your family for one year?
- Working as a group to determine the answer to this question, students should be organized into pairs to share a calculator but each using their own journal to record the calculations developed on the whiteboard.
- Using the whiteboard space efficiently, use the “Calculations Group Equation Sequence” page:
- Pose all text and questions, written in italics, verbally to the group.
- Write the bolded questions on the whiteboard.
- Write the equations that correspond to the question on the board,in a tidy column.
- After each question, allow students a short time (10–20 seconds) to try doing the equations on their calculators, then write the correct answer on the board before moving onto the next question.
- Be sure to write out the equations exactly as they appear on the “Calculations Group Equation Sequence” page, with their associated units of measure, so that students do not lose sight of the question or the meaning of the answers.
Closing Circle
Conclusions from the Math Narrative:
How much corn would you need to feed a family for one year?
902,720 grams, or 11,284 ears
How many clumps of corn would that take?
1,128 clumps
How much field space would need to be planted, using only a so’ya/digging stick, to grow that number of clumps of corn?
4,512 square meters
CO Standards
This lesson plan was designed to align with the following Montezuma School to Farm Project Garden Education Standards and state Of Colorado Academic Standards:
| Montezuma School to Farm Project’s Garden Education Standards | Colorado Academic Standards | |
| 6th |
Intro to garden mapping and planning.
Ancestral Puebloan agricultural practices |
Science 2.1, 2.2, 3.3 Math 1.1, 1.2, 2.1, 2.2, 4.1 Health 2.1, 2.2 Phys Ed 1.2, 3.1, 3.2 Social Studies 1.1, 1.2, 2.2, 3.1 Reading/Writing/Communicating 1.1, 4.3 |
| 7th |
Irrigation and water conservation Sustainable water use practices and devices |
Science 2.1 Math 1.1, 1.2, 2.2, 4.1, 4.2 Health 2.1, 3.1 Phys Ed 3.2 Social Studies 2.2 Reading/Writing/Communicating 1.2 |
| 8th |
Soil ecology: interconnectedness of soil health and human health Innovative irrigation practices Hand and power tools Deep understanding of water as a precious and limited resource Changing systems: climate and weather in the Southwest |
Science 2.1 Math 2.2, 4.2 Health Phys Ed Social Studies 2.2 Reading/Writing/Communicating 1.2 |
Further information in regards to the Colorado State Standards may be found here.
Handout: Calculation Sequence
- Pose all text and questions, written in italics, verbally to the group.
- Write the bolded questions on the board.
- Write the equations that correspond to the question on the board, in a tidy column.
- Allow students (10–20 seconds) to try the equation on calculators; then write correct answer the board.
- Write out the equations exactly as they appear, with their associated units of measure.
How much corn would you need to feed yourself and your family for one year?
To have a healthy body, a person needs to eat about 2000 calories (Cal) each day. If you came from an ancestral Pueblo household, 75% of the food you ate every day came from corn. This would mean that you get 75% of your calories from corn.
How many grams of corn would each person need to eat each day to fulfill 75% of their diet?
What is 75% of 2000 calories?
\[2000 \text{ Cal} \times 0.75 = 1500 \text{ Cal}\]
1500 daily calories would come from corn, per person.
How many grams of dried whole kernels of corn would give you 1500 calories, if we know that 100 grams of dried whole kernel corn provides approximately 375 calories?
\[1500 \text{ Cal} \div 375 \text{ Cal} = 4\] \[4 \times 100 \text{ grams} = 400 \text{ grams}\]
This means you would need to eat 100 grams of corn four times each day to reach 1500 calories. 400 grams of corn need to be eaten by each person in the household everyday, for them to gain 1500 calories. Show the students four 100 gram bags.
How many grams of corn kernels would be needed for food by a household every day?
Survey the students: How many people eat meals at your home on any given day? Calculate the average number of people in a household, as represented by this student group. The calculations below have used an average of 4 people per household.
How many grams of corn kernels are needed to feed a household of four people, per day?
Remember, these grams of food (made from corn) would come from plants you grow, on dryland farms, not from food bought at the store.
And, it is only 75% of the food needed for the day; for example, we can think of 1600 grams as providing for breakfast and lunch not dinner.
Multiply the answer to Question A X 400 grams to find the number of grams of corn kernels needed everyday by the household.
\[ 4 \text{ persons} \times \frac{400 \text{ grams}}{1 \text{ person}} = 1600 \text{ grams}\]
1600 grams of corn kernels are needed by a household of four people every day.
How many grams of corn kernels are needed for food by this household every year?
Multiply the answer to Question B X 7 days in a week.
\[\frac{1600\text{ grams}}{1\text{ day}}\times\frac{7\text{ days}}{1\text{ week}}=\frac{11200\text{ grams}}{1 \text{ week}}\]
11,200 grams of corn kernels are needed by a household of four people every week.
Multiply the answer to Question C X number of weeks in a year:
\[\frac{11200\text{ grams}}{1\text{ week}}\times\frac{52\text{ weeks}}{1\text{ year}}=\frac{582400\text{ grams}}{1 \text{ year}}\]
582,400 grams of corn kernels are needed by a household of four people every year.
In a Hopi household, an additional 5% more corn is needed for days of ceremony, holidays and feasts. For example:, a wedding, a birth.
Multiply the answer to Question D X 5% or 0.05:
\[\frac{582400\text{ grams}}{1\text{ year}}\times0.05=\frac{29120\text{ grams}}{1 \text{ year}}\]
29,120 grams of extra corn kernels are needed by a household of four people every year for ceremonies, holidays and feasts.
In a Hopi household, an additional 50% more corn is grown in order to stock up on seed for the future and to prepare for drought years.
Multiply the answer to Question D X 50% or 0.50:
\[\frac{582400\text{ grams}}{1\text{ year}}\times0.5=\frac{291200 \text{ grams}}{1 \text{ year}}\]
291,200 grams of extra corn kernels are needed by a household of four people every year for seed stock.
Add the answers to Questions D + E + F to find the total number of grams of corn you must grow each year to provide for the needs of a Hopi family of four people.
\[\frac{582400\text{ grams}}{1\text{ year}}+\frac{29120\text{ grams}}{1\text{ year}}+\frac{291200\text{ grams}}{1\text{ year}}=\frac{902720 \text{ grams}}{1 \text{ year}}\]
902,720 grams of corn kernels are needed by a household of four people every year.
How many ears of corn would provide this many grams of corn kernels?
1.25 ears of corn has an average of 100 grams of whole kernels.
Multiply the answer to Question G X 1.25 ears per 100 grams:
\[\frac{902720\text{ grams}}{1\text{ year}}\times\frac{1.25\text{ ears}}{100\text{ grams}}=\frac{11284\text{ ears}}{1 \text{ year}}\]
11,284 ears of corn are needed by a household of four people every year.
How many corn plants would provide this many ears of corn?
Each stalk of corn typically produces 2 ears.
Multiply the answer to Question H by 1 plant per 2 ears:
\[\frac{11284\text{ ears}}{1\text{ year}}\times\frac{1\text{ plant}}{2\text{ ears}}=\frac{5642\text{ plants}}{1 \text{ year}}\]
5,642 corn plants are needed by a household of four people every year.
How many corn clumps would provide this many corn plants?
Hopi people grow corn plants in clumps of approximately 5 corn plants each.
Multiply the answer to Question I by 1 clump per 5 ears:
\[\frac{5642\text{ plants}}{1\text{ year}}\times\frac{1\text{ clump}}{5\text{ plants}}=\frac{1128\text{ clumps}}{1 \text{ year}}\]
1,128 clumps are needed by a household of four people every year.
How much field space would a family need to plant to have enough corn?
Hopi people plant clumps approximately 2 meters (m) apart; each clump needs about 4 m2 of space. Multiply the answer to Question J by 4 m2 and conclude by viewing “Diagram 2: An American Football Field” and return to “Closing Circle” section of lesson plan.
\[\frac{1128\text{ clumps}}{1\text{ year}}\times\frac{4\text{ m}^2}{1\text{ clump}}=\frac{4512\text{ m}^2}{1 \text{ year}}\]